TD5 : Réseau feedforward avec synapses plastiques¶
1. Réseau feedforward¶
Considérons un réseau feedforward avec une couche de 1000 neurones d'entrée et un neurone de sortie. Le lien entre chaque neurone présynaptique, $i \in (1,1000)$, et le neurone postsynaptique a un poids $w_j$. Tous les neurones de ce réseau sont binaires, ils peuvent être actifs $x_j(t_i)=1$ ou inactifs $x_j(t_i)=0$ à chaque instant.
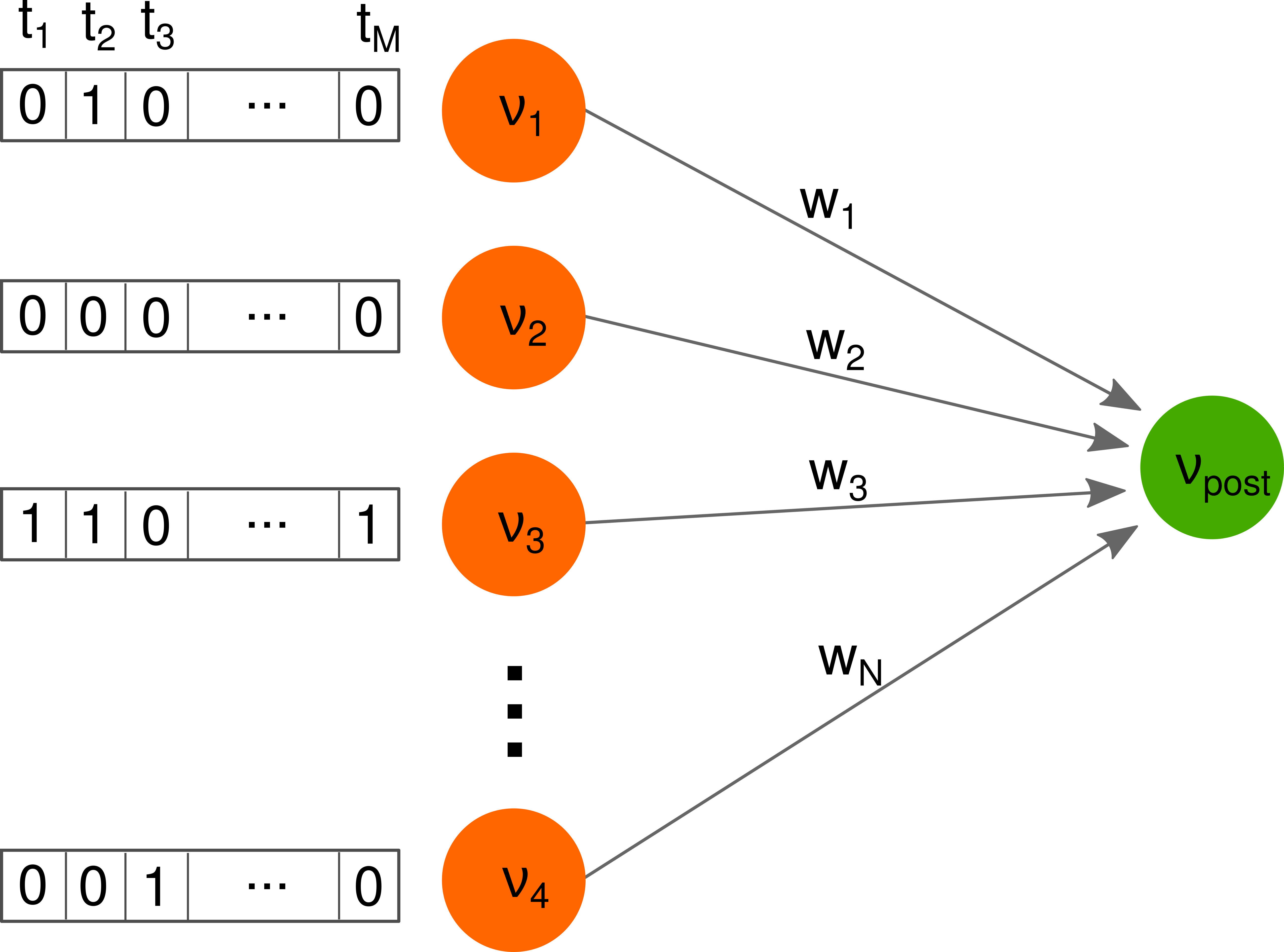L'activité des neurones postsynaptiques à chaque instant est donnée par la somme de toutes les activités présynaptiques multiplié par le poids synaptique :
$$y(t_i) = \Theta \left( \sum_j w_j * x_j(t_i) - 0.5 \right).$$
La fonction heaviside $\Theta$ est définie comme suit : $\Theta(x) = 0$ si $x<0$, et $\Theta(x) = 1$ if $x\geq0$.
Indice : Pour décrire l'activité présynaptique, diviser le vecteur temps en petits intervalles $dt$. Pour chaque intervalle, un neurone peut être actif $1$ ou inactif $0$.
E1 Créer une activité présynaptique irrégulière.¶
Commencez par créer des vecteurs d'activité pour tous les neurones présynaptiques pendant une durée totale de $10$ secondes et avec un intervalle de $0.1$ ms. Chaque neurone devrait déclencher des spikes irrégulières à $\nu = 10$ Hz. Pour ce faire, tirez autant de nombres aléatoires $\eta_i \in [0,1]$ que d'intervalles de temps et décidez pour chaque intervalle si le neurone est actif ou inactif sur la base de la comparaison suivante : neurone actif $x_j(t_i) = 1$ si $\eta_j(t_i) < \nu * dt$ and inactif $x_j(t_i) = 0$ sinon.
Calculez la taux de décharge et le coefficient de variation pour chaque neurone.
E2 calculer l'activité postsynaptique¶
L'activité postsynaptique est une fonction de l'activité présynaptique et de l'architecture du réseau. Exécuter le réseau et calculer l'activité postsynaptique pour chaque intervalle.
Indice : Faites un cycle dans le temps et calculez l'activité postsynaptique pour chaque intervalle de temps en fonction de la somme de toutes les activités présynaptiques multipliées par le vecteur de poids. Initialisez tous les poids synaptiques à $0.1$.
Quelle est le taux de décharge approximative du neurone postsynaptique ? Et quel est son coefficient de variation ? Comment le taux de décharge et le coefficient de variation changent-ils si le poids est augmenté à $0.12$ pour tous les synapses.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
nPreNeurons = 1000
T = 10.
dt = 0.0001
timeBins = int(T/dt)
r = 10.
tTime = np.linspace(dt,dt*timeBins,timeBins)
preActivity = np.zeros((nPreNeurons,timeBins))
synapticWeights = np.ones(nPreNeurons)*0.12 #np.random.rand(nPreNeurons)
#synapticWeights = np.random.rand(nPreNeurons)*0.2
#####################################################
# create presynaptic activity : attribute spikes to each presynaptic neuron
for i in range(nPreNeurons):
randomNumbers = np.random.rand(timeBins)
preActivity[i][randomNumbers<r*dt] = 1
#####################################################
# statistics of the pre-synpatic spike trains
for i in range(nPreNeurons):
spikes = tTime[preActivity[i]==1]
ISIs = spikes[1:]-spikes[:-1]
meanISI = np.mean(ISIs)
sdISI = np.std(ISIs)
if i < 10:
print('mean firing rate of neuron %s is %0.3f Hz, and CV is %0.3f' % (i,1./meanISI,sdISI/meanISI))
#####################################################
# calculate dynamics of the feedforward network
postActivity = np.zeros(timeBins)
print('running network simulation ... ',)
for i in range(timeBins):
preInput = sum(preActivity[:,i]*synapticWeights)
if preInput > 0.5:
postActivity[i] = 1.
else:
postActivity[i] = 0.
if not (i%(1./dt)):
print('%s s simulated' % (i//(1./dt)))
#####################################################
# statistics of the post-synpatic spike trains
if sum(postActivity)>0:
postSpikes = tTime[postActivity==1]
postISIs = postSpikes[1:]-postSpikes[:-1]
meanISI = np.mean(postISIs)
sdISI = np.std(postISIs)
print('mean firing rate of the post-synaptic neuron is %0.3f Hz, and CV is %0.3f' % (1./meanISI,sdISI/meanISI))
else:
print('the postsynaptic neuron is not active')
Pour $w = 0.1$, le taux de decharge moyenne est $\nu_{post} \approx 5.5$ Hz.
Pour $w = 0.12$, le taux de decharge moyenne est $\nu_{post} \approx 35$ Hz.
E3 Synapses plastiques¶
Nous introduisons maintenant une mise à jour du poids synaptique en fonction de l'activité pre- et postsynaptique. Le poids d'une synapse est augmenté par $\eta=0.005$ si les deux neurones pré- et postsynaptiques sont actifs dans le même intervalle de temps. $$ w_j(t_{i+1}) = w_j(t_i) + \eta \,\,\, \rm{if} \,\,\, y(t_i)=1 \,\, \rm{and} \,\, x_j(t_i)=1$$ Sinon, si les neurones pré- ou postsynaptiques sont actifs seuls, le poids synaptique est diminué par $\eta$. $$ w_j(t_{i+1}) = w_j(t_i) - \eta \,\,\, \rm{if} \,\,\, y(t_i)=1 \,\, \rm{and} \,\, x_j(t_i)=0$$ ou $$ w_j(t_{i+1}) = w_j(t_i) - \eta \,\,\, \rm{if} \,\,\, y(t_i)=0 \,\, \rm{and} \,\, x_j(t_i)=1$$
Le poids synaptique reste constant en l'absence d'activité.
Initialiser à nouveau tous les poids synaptiques à $0.1$ et effectuer la simulation pendant $10$ s avec un pas de temps de $0.1$ ms. Comme avant, Tous les neurones présynaptiques sont actifs de façon irrégulière et leur taux de décharge est à 10 Hz.
A quoi ressemble la distribution du poids synaptique à la fin de la simulation ?
Comment cette distribution change-t-elle si $100$ neurones déclenchent des spikes synchrones tout au long de la simulation (toujours à 10 Hz)?
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
nPreNeurons = 1000
T = 10.
dt = 0.0001
timeBins = int(T/dt)
r = 20.
tTime = np.linspace(dt,dt*timeBins,timeBins)
# learning parameters
eta = 0.005
interestingNeurons = 0
preActivity = np.zeros((nPreNeurons,timeBins))
synapticWeights = np.zeros((nPreNeurons,timeBins))
initialWeights = np.ones(nPreNeurons)*0.1 #np.random.rand(nPreNeurons)
#synapticWeights = np.random.rand(nPreNeurons)*0.3
synapticWeights[:,0] = np.copy(initialWeights)
#####################################################
# create presynaptic activity : attribute spikes to each presynaptic neuron
# first 'interestingNeurons' firing synhronous action potentials
randomNumbers = np.random.rand(timeBins)
for i in range(interestingNeurons):
preActivity[i][randomNumbers<r*dt] = 1.
# rest of the neurons : not synchronous
for i in range(interestingNeurons,nPreNeurons):
randomNumbers = np.random.rand(timeBins)
preActivity[i][randomNumbers<r*dt] = 1.
#####################################################
# statistics of the pre-synpatic spike trains
for i in range(nPreNeurons):
spikes = tTime[preActivity[i]==1]
ISIs = spikes[1:]-spikes[:-1]
meanISI = np.mean(ISIs)
sdISI = np.std(ISIs)
if i < 10:
print('mean firing rate of neuron %s is %0.3f Hz, and CV is %0.3f' % (i,1./meanISI,sdISI/meanISI))
#####################################################
# calculate dynamics of the feedforward network
postActivity = np.zeros(timeBins)
print('running network simulation ... ',)
for i in range(timeBins-1):
preInput = sum(preActivity[:,i]*synapticWeights[:,i])
if preInput > 0.5:
postActivity[i] = 1.
else:
postActivity[i] = 0.
# update synaptic weights
# synaptic increase LTP
# was presynaptic spike fired during the LTP window
if i < (timeBins-1):
synapticWeights[:,(i+1)] = synapticWeights[:,i]
if postActivity[i]==1.:
LTPmask = (preActivity[:,i]==1)
synapticWeights[:,(i+1)][LTPmask] = synapticWeights[:,i][LTPmask]+eta
synapticWeights[:,(i+1)][synapticWeights[:,(i+1)]>1.]=1.
#
LTDmask = (preActivity[:,i]==0)
synapticWeights[:,(i+1)][LTDmask] = synapticWeights[:,i][LTDmask]-eta
synapticWeights[:,(i+1)][synapticWeights[:,(i+1)]<0.]=0.
elif postActivity[i]==0.:
LTDmask2 = (preActivity[:,i]==1)
synapticWeights[:,(i+1)][LTDmask2] = synapticWeights[:,i][LTDmask2]-eta
synapticWeights[:,(i+1)][synapticWeights[:,(i+1)]<0.]=0.
#if np.any(postActivity[(i-nLTD):i]):
# LTDmask = (preActivity[:,i]==1.)
# #print(sum(LTDmask))
# synapticWeights[LTDmask]-=eta
# synapticWeights[synapticWeights<0.]=0.
if not (i%(1./dt)):
print('%s s simulated' % (i//(1./dt)))
#####################################################
# statistics of the post-synpatic spike trains
if sum(postActivity)>0:
postSpikes = tTime[postActivity==1]
postISIs = postSpikes[1:]-postSpikes[:-1]
meanISI = np.mean(postISIs)
sdISI = np.std(postISIs)
print('mean firing rate of the post-synaptic neuron is %0.3f Hz, and CV is %0.3f' % (1./meanISI,sdISI/meanISI))
else:
print('the postsynaptic neuron is not active')
#plt.hist(initialWeights,bins=100)
plt.hist(synapticWeights[:,-1],bins=50)
#plt.hist(synapticWeights,bins=50,la)
plt.plot(tTime,np.mean(synapticWeights[:interestingNeurons],0))
plt.plot(tTime,np.mean(synapticWeights[interestingNeurons:],0))
Tous les poids synaptiques sont déprimés, du poids 0, à la fin de la simulation.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
nPreNeurons = 1000
T = 10.
dt = 0.0001
timeBins = int(T/dt)
r = 20.
tTime = np.linspace(dt,dt*timeBins,timeBins)
# learning parameters
eta = 0.005
interestingNeurons = 100
preActivity = np.zeros((nPreNeurons,timeBins))
synapticWeights = np.zeros((nPreNeurons,timeBins))
initialWeights = np.ones(nPreNeurons)*0.1 #np.random.rand(nPreNeurons)
#synapticWeights = np.random.rand(nPreNeurons)*0.3
synapticWeights[:,0] = np.copy(initialWeights)
#####################################################
# create presynaptic activity : attribute spikes to each presynaptic neuron
# first 'interestingNeurons' firing synhronous action potentials
randomNumbers = np.random.rand(timeBins)
for i in range(interestingNeurons):
preActivity[i][randomNumbers<r*dt] = 1.
# rest of the neurons : not synchronous
for i in range(interestingNeurons,nPreNeurons):
randomNumbers = np.random.rand(timeBins)
preActivity[i][randomNumbers<r*dt] = 1.
#####################################################
# statistics of the pre-synpatic spike trains
for i in range(nPreNeurons):
spikes = tTime[preActivity[i]==1]
ISIs = spikes[1:]-spikes[:-1]
meanISI = np.mean(ISIs)
sdISI = np.std(ISIs)
if i < 10:
print('mean firing rate of neuron %s is %0.3f Hz, and CV is %0.3f' % (i,1./meanISI,sdISI/meanISI))
#####################################################
# calculate dynamics of the feedforward network
postActivity = np.zeros(timeBins)
print('running network simulation ... ',)
for i in range(timeBins-1):
preInput = sum(preActivity[:,i]*synapticWeights[:,i])
if preInput > 0.5:
postActivity[i] = 1.
else:
postActivity[i] = 0.
# update synaptic weights
# synaptic increase LTP
# was presynaptic spike fired during the LTP window
if i < (timeBins-1):
synapticWeights[:,(i+1)] = synapticWeights[:,i]
if postActivity[i]==1.:
LTPmask = (preActivity[:,i]==1)
synapticWeights[:,(i+1)][LTPmask] = synapticWeights[:,i][LTPmask]+eta
synapticWeights[:,(i+1)][synapticWeights[:,(i+1)]>1.]=1.
#
LTDmask = (preActivity[:,i]==0)
synapticWeights[:,(i+1)][LTDmask] = synapticWeights[:,i][LTDmask]-eta
synapticWeights[:,(i+1)][synapticWeights[:,(i+1)]<0.]=0.
elif postActivity[i]==0.:
LTDmask2 = (preActivity[:,i]==1)
synapticWeights[:,(i+1)][LTDmask2] = synapticWeights[:,i][LTDmask2]-eta
synapticWeights[:,(i+1)][synapticWeights[:,(i+1)]<0.]=0.
#if np.any(postActivity[(i-nLTD):i]):
# LTDmask = (preActivity[:,i]==1.)
# #print(sum(LTDmask))
# synapticWeights[LTDmask]-=eta
# synapticWeights[synapticWeights<0.]=0.
if not (i%(1./dt)):
print('%s s simulated' % (i//(1./dt)))
#####################################################
# statistics of the post-synpatic spike trains
if sum(postActivity)>0:
postSpikes = tTime[postActivity==1]
postISIs = postSpikes[1:]-postSpikes[:-1]
meanISI = np.mean(postISIs)
sdISI = np.std(postISIs)
print('mean firing rate of the post-synaptic neuron is %0.3f Hz, and CV is %0.3f' % (1./meanISI,sdISI/meanISI))
else:
print('the postsynaptic neuron is not active')
#plt.hist(initialWeights,bins=100)
plt.hist(synapticWeights[:,-1],bins=50)
#plt.hist(synapticWeights,bins=50,la)
plt.plot(tTime,np.mean(synapticWeights[:interestingNeurons],0))
plt.plot(tTime,np.mean(synapticWeights[interestingNeurons:],0))
Les poids de la population synchrone sont 1 et le reste des poids sont 0.